IBM i のウンチクを語ろう:その66
- 量子コンピュータ奇々怪々 -
皆さん、こんにちは。「最近よく話題になるのだけれど、Webサイトや本を読んでもさっぱり仕組みがわからない・・・」という同僚のコメントがきっかけとなって、毎月開催されている社内向け勉強会にて、量子コンピュータをテーマとして取り上げる事にしてしまいました。私はここで毎回IBM i に関わるネタを提供しているのですが、世間で話題のネタもついでにカバーできないかと打診されたというわけです。だからと言って私に量子コンピュータに関して何らかの経験があったわけではありません。「重ね合わせ」とか「もつれ」など、言葉だけは聞いた事はあるといった程度ですし、0か1かの値が決まっていない量子ビットを相手に演算を行うことで、なぜ特定の結果が得られるのか、私にとってもミステリーでしかありません。そのうちに機会があったら調べようかなと一旦脇に押しやったままにしておいたのですが、どうやら潮時がやって来たようです。
そもそも量子物理学とは無縁の経済学士に向かって、無茶な要求にも思えるのですが、それなりに何とかできるだろうと私の方も安易に構えていたのも事実です。受けたからには勉強会に向けて準備を進めなくてはなりません。やおら初心者向けの本やらWebサイトやらを読み散らかし始めたわけですが、当初は1日かけても1ミリも理解が進むことはなく、迂闊な判断だったと呆然とするだけで終わってしまっておりました。このままではまずいと何日も時間をかけて調べ続けた挙句、「まあ、こんなものなのだろうか」といった妥協点に何とか到達できたような気がします。それにしても「入門」とか「やさしい」を標榜しているにもかかわらず、文系向けにもっとわかりやすく説明してくれても良かったのに、と恨めしく思う説明に何度も出くわしました。そこで今回は、量子コンピュータに関するいくつかのポイントについて、こう思っておけばどうやら都合が良さそうだ、といった我流の解釈と共に、現状について認識を改めた点をお伝えしようと思います。私と似たような状況に陥っている方に、多少なりともより明確なイメージを抱いていただけるようになる事が目的です。
従来のコンピュータにおける最小の情報単位はビットと呼ばれ、必ず0か1のどちらかの値をとる、ということは皆様ご存知のとおりです。これに対して量子ビットは「0か1かは決まっておらず、両者が重ね合わされた状態にある」といった説明をよく見ます。私はまずここで躓きました。異なる値がスライドのように「重ね合わされる」とは一体どういう事か、入門書でもあまり説明もなされないか、下手をするとわけのわからない図や数式が続きます。
ここでは0と1それぞれが出現率を伴っている、といった具合に確率の考え方を持ち込むと都合が良いようです。我々が知っているビットというのは必ず0か1かの値を取りますので、100%の0と0%の1、または0%の0と100%の1、のどちらかの組み合わせのみが存在しています。そして何らかの操作をしない限り、何度参照しても0のものは常に0です。これに対して量子ビットにおいては中途半端な組み合わせが無限にあり得ます。30%の0と70%の1も有効ですし、30.5%の0と69.5%の1でも良いわけです。「重ね合わせ」とはどうやらこんな組合せのことです。そして10回参照すれば0は3回、1は7回観測されるかもしれません。従来のビットは折り目正しく筋が通っている(?)のに対して、量子ビットはいつもフラフラしています。一体どっちなんだと問い詰められると、場当たり的に出現確率にしたがって0か1を答えるいい加減なヤツだと思えば良さそうです。
0か1かは決まっていませんが、それぞれの出現率を設定・操作することはできるようです。値として確定させるのであれば、従来ビット同様に出現率100%の0とか1とすれば良いでしょうし、未定の状態であれば50%ずつの0と1とすれば済みます。量子演算の中にはこの確率操作も含まれています。例えば演算結果が70%の確率で0になるというのでは心もとないですが、操作することでこれが限りなく100%に近付くのであれば、確定値として採用するので良さそうです。
量子は粒であるばかりでなく波でもある、といった説明もよく目にします。そして直感的に理解し易いからという理由で、ブロッホ球が続いて紹介されます。下の地球儀のような図をご覧になったことがある方も多いのではないでしょうか。私にとってはこいつが曲者で、当初これは量子の模型なのだろうと思い込んでおりました。球内の矢印の先端部分が示す、地球の緯度に相当する箇所が0と1の出現確率を表していることは直感的にわかります。北極を指していれば100%の0、南極ならば100%の1、日本付近ならばおよそ7-80%の0と2-30%の1、といった具合です。ただ、波であるはずの0と1はこの球の中でどのように表現されるのか、という点が最大の謎でした。どの本・Webサイトを紐解いて探し回っても、それらしい説明を見つけることができません。
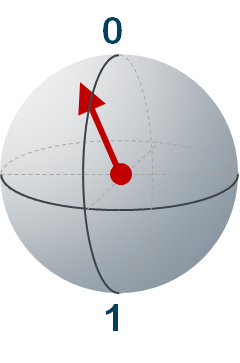
散々悩んだ末の結論は、ゴチャゴチャするから描ききれない、というものです。本来はおそらく0には0の、1には1の、確率を決定するための波を示す矢印があって、両者を足し合わせたものが球内に記された矢印です。「足し合わせた」とは言っても、3+4=7のような単純な加算ではなく、矢印が指し示す方向も考慮しなければなりません。3+4の例で言うと、互いにちょうど正反対を向けば加算結果は1になりますし、直角の方向を向けば5です。昔数学で習ったベクトルでは、こんな不思議な計算をしていたことを思い出します。うっかり量子物理学の本を開くと、複素数とか三角関数を用いて表現されたベクトルが登場します。量子演算とは矢印を様々に回転させることであり、その回転は行列演算で表現されます。頭痛がしますね。数学的裏付けをもって量子を理解しようとするならば、このブロッホ球は有効な手段なのでしょうけれども、わかったような気がすることが目的ならば、大して役立つとは思えませんでした。あちこちで紹介されているので、私自身も大分惑わされたような気がします。
量子コンピュータでは「量子の0と1とが重ね合わされた状態のまま演算を行うから、解決するべき問題次第では演算回数を劇的に削減することができる」、といったような説明を見かけます。これだけでは何の事だかさっぱりわかりませんでした。0と1の出現率がそれぞれ50%ずつの量子ビットを相手に演算を行ったところで、結果もやはり出現率50%ずつの0と1になるのではないか、だとしたら何の意味があるのか、という理屈です。
このちょっとした混乱は、従来型コンピュータのアルゴリズム(演算処理手順)に囚われていて、それを量子コンピュータに適用しようとする事から生じていると言えそうです。従来型コンピュータには従来型コンピュータ用のアルゴリズムがあるのと同様に、量子コンピュータには量子コンピュータ用のアルゴリズム、先の表現で言うとブロッホ球内矢印の回転のさせ方に相当する手続きがあります。そもそも情報を保持するビットの振舞いが全く異なるので、アルゴリズムが共通にはならないのは致し方無いことです。従来型コンピュータでは解けない問題が解けるようになるのも、演算回数を劇的に削減するアルゴリズムによるものです。そしてこれまでに発見されたアルゴリズムはQuantum Algorithm Zooに公開されており、数えてみると現時点で60超ほどあります。逆に言うとこれしか見つかっていないとも言えそうですが。

念のためですが、量子コンピュータを利用することで個々の演算を高速化できるという主張は、私が目にした書籍やWebサイトのどこにもありません。未だ実用化されたわけではないので、従来型コンピュータに比べて演算速度がどうなるのかはわからない、現時点ではとりあえず同等程度と見なしておく、といったような記述があったくらいです。量子コンピュータは必ずしも速くはないようです。
量子コンピュータに適した問題とは、従来のコンピュータでは演算回数が多過ぎてしまい解くことが困難なもの、そして演算回数を大幅に削減できるような、効果的なアルゴリズムが発見されているものに限定されます。ですから私達が日頃接している基幹業務アプリケーションがその対象になる可能性はまず無さそうです。
量子コンピュータがそのパワーを発揮すると言われている有名な問題の例の一つは、自然数を素数の積に分解する素因数分解です。例えば15=3×5程度であればすぐに答えがわかりますが、731を見て直ぐに答えられる方はいらっしゃらないでしょう。筆算であれ従来型のコンピュータ利用であれ、小さい素数からしらみつぶし的に割算を試してみるしか良い解法がありません。そしてようやく731=17×43に到達できます。もしこの数が数100桁に及ぶような大きな数になると、コンピュータを使っても現実的に解く事はできません。一方で掛け算を行えば、得られた答えが正しいことを簡単に検証できます。この一方通行的な特性が、世間で広く使われているRSA暗号成立の前提になっています。量子コンピュータを利用する場合にはショア(Peter Shor)のアルゴリズムなるものが既に発見されていて、素因数分解の解法が判明しているそうです。興味のある方はWeb検索すると文書が多数ヒットしますので、ご参照いただければと思います。私にはさっぱり、でしたが。

素因数分解の解法が見つかっているという事は、世の中の暗号が成立する前提が既に崩れていて、全て丸裸状態にあるのかというと未だそうはなっていません。アルゴリズムの研究は進んでいる一方で、量子コンピュータが扱えるビット数は、実用化するにはまだまだ少な過ぎるのが大きな理由です。私が目にした文章の中には、実用化のためには少なくとも百万から一億ビットが必要になるだろう、といった観測が述べられていました。例えばIBM製量子コンピュータであるIBM Qのサイトを見ると、今年127ビット(先の11月16日にEagleが発表されています)、来年433ビット(Osprey)、再来年1121ビット(Condor)、その後百万ビット超を目指すといったロードマップが描かれています。また量子コンピュータでもビットエラーは発生し得るので、それを訂正する仕組みも組み込まなければなりません。
実装方法も現時点では決定打と言われるものはありません。巨大冷凍庫が印象的なIBM Qは超電導方式、すなわち金属などを絶対零度(-273.15°C)にまで冷却すると、抵抗値がゼロになり、電子が自由に動き回れるようになる現象を利用しています。他にもイオン方式や光方式などがあり、それなりに大掛かりな装置になるようです。それぞれに量子ビット数の大規模化、エラー発生率、量子測定のし易さなどに一長一短があります。いずれにせよIBM i のように、企業が自社用に導入するタイプのシステムではなさそうです。
現在の暗号が無効化されてしまったら、社会に絶大な影響を与えます。これを回避するために、量子コンピュータをもってしても解読不能とされる耐量子暗号なるものも既に登場しています。一方で、計算回数が大き過ぎるために、スパコンを使っても解けなかった問題が解決される事も期待されます。何年後になるのか皆目見当もつきませんが、いずれ量子コンピュータが実用化された時に、社会の景色がどう変化するのか楽しみですね。
ではまた。










