SQLで連続データを生成する
私の仕事のほとんどは、平凡で、いつも変わらない、ほぼ同じことの繰り返しです。文句を言っているわけではありません。日々の生活のほとんどは、ありふれたお決まりのことばかりですが、そうであるべきものなのでしょう。砂糖をかけ過ぎると、ケーキは台無しになります。けれども、時には、難題にぶつかることもあります。そのようなときには、プログラミングが楽しみになることもあります。
今回の記事は、そのような経験から生まれたものです。1週間分の日付が入った表が必要になりました。RPGプログラムを書いてもよかったのですが、SQLがこのタスクを処理できることも分かっていました。この記事では、連続する整数および日付を生成するのに使用できる2つの手法を紹介します。その他のデータ タイプへの適応については皆さんにお任せします。
2つの生成メカニズム
SQLに連続データを生成させるメカニズムとして、オラクル方式(私はCONNECT BYをそう呼んでいます。私が知るところではOracle社発だからです)と、再帰的共通表式という2つのメカニズムがあるようです。それぞれのメカニズムについて、1~10の整数の表を生成させることを通じて説明しようと思います。まずは、オラクル方式(CONNECT BY)を以下に示します。
declare global temporary table Seq as
(with series as
(select level as n
from sysibm.sysdummy1
connect by level <= 10)
select * from series)
with data;CONNECT BY節はありますが、START WITHはないことに注目してください。また、CONNECT BYが、データベースが自動的に生成する変数であるLEVELを参照していることにも注目してください。これがどのように動作し、どうして動作するかについて様々な解説を読みましたが、私にとって十分満足のいくように分かりやすく説明してくれているものはありませんでした。結果は以下の表です。
| N |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
以上が、連続データを生成する1つの方法です。また、再帰的共通表式を使用しても、同じ表を生成することができます。
with series (n) as
(select 1 from sysibm.sysdummy1
union all
select (n + 1) from series
where n < 10)
select * from series1つ目のSELECTは、照会に数値1を提供します。2つ目のSELECT(UNION ALLの後)は、2~10の値の行を生成します。結果として生成される表は、前の照会の表と同じです。
他のタイプのデータを生成する
これらの照会を、他のタイプのデータを生成するための土台として利用することができます。ある日付を指定して、その日付とそれに続く6つの日付(つまり1週間分の日付)を含む表を生成してみましょう。オラクル方式を以下に示します。
declare global temporary table WeekOfDatesA as
(with dates (dt) as
(select date('2020-03-16') + (level -1) days
from sysibm.sysdummy1
connect by level <= 7 )
select * from dates)
with data
with replace;以下が出力です。
| DT |
| 2020-03-16 |
| 2020-03-17 |
| 2020-03-18 |
| 2020-03-19 |
| 2020-03-20 |
| 2020-03-21 |
| 2020-03-22 |
これは、整数の連続データを生成した手法のバリエーションです。生成された整数値を日付計算に使用して日付を生成しました。
再帰的CTEの手法については、ここでは示さないこととします。そちらでも行うことはできるのですが、私が思い付いたバリエーションは、どれも気に入らないものばかりでした。すっきりとした手法を思い付いた方がいらしたら、ぜひ、お教えください。
パズルで遊ぶ
私が知る限りでは実用的な価値はありませんが、あるイラストを紹介したいと思います。ある日、他のものを探していて偶然見つけたものです。それはSQLを使用した エイト クイーン パズルの解法です。
私がエイト クイーン パズルを知ったのは、大学でコンピューター サイエンスの学位取得を目指していたときでした。このパズルを解くためにPascalプログラムを書く必要がありました。このパズルを、SQLを使用して解くことができるとはまったく思い付かなかったのですが、ある日、 Quoraに投稿されているのを見つけたというわけです。
このパズルのルールは、チェス盤に8個のクイーンの駒を置き、どの駒もお互いに取られない位置に配置するというものです。つまり、2つのクイーンは、チェス盤の同じ「ランク(横の段)」(行)、同じ「ファイル(縦の列)」(列)、または同じ「ダイアゴナル(斜めの筋)」上に置くことができません。解は92通りあります。その1つの解が以下の図です。
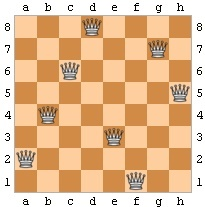
以下は、私が編み出した解法です。
with ta as (select level as a
from sysibm.sysdummy1
connect by level <= 8),
tb as (select a as b from ta),
tc as (select a as c from ta),
td as (select a as d from ta),
te as (select a as e from ta),
tf as (select a as f from ta),
tg as (select a as g from ta),
th as (select a as h from ta)
select a, b, c, d, e, f, g, h
from ta cross join tb
cross join tc cross join td
cross join te cross join tf
cross join tg cross join th
/* check for same rank (row) */
where a <> b and a <> c and a <> d and a <> e
and a <> f and a <> g and a <> h and b <> c
and b <> d and b <> e and b <> f and b <> g
and b <> h and c <> d and c <> e and c <> f
and c <> g and c <> h and d <> e and d <> f
and d <> g and d <> h and e <> f and e <> g
and e <> h and f <> g and f <> h and g <> h
/* check for same ascending diagonal */
and a+1 <> b and a+2 <> c and a+3 <> d
and a+4 <> e and a+5 <> f and a+6 <> g
and a+7 <> h and b+1 <> c and b+2 <> d
and b+3 <> e and b+4 <> f and b+5 <> g
and b+6 <> h and c+1 <> d and c+2 <> e
and c+3 <> f and c+4 <> g and c+5 <> h
and d+1 <> e and d+2 <> f and d+3 <> g
and d+4 <> h and e+1 <> f and e+2 <> g
and e+3 <> h and f+1 <> g and f+2 <> h
and g+1 <> h
/* check for same descending diagonal */
and a-1 <> b and a-2 <> c and a-3 <> d
and a-4 <> e and a-5 <> f and a-6 <> g
and a-7 <> h and b-1 <> c and b-2 <> d
and b-3 <> e and b-4 <> f and b-5 <> g
and b-6 <> h and c-1 <> d and c-2 <> e
and c-3 <> f and c-4 <> g and c-5 <> h
and d-1 <> e and d-2 <> f and d-3 <> g
and d-4 <> h and e-1 <> f and e-2 <> g
and e-3 <> h and f-1 <> g and f-2 <> h
and g-1 <> h
order by a, b, c, d, e, f, g, h- オラクル方式を使用して、共通表式TAで1~8の数値を生成します。
- TAを、TB~THの7つの共通表式に複製します。これにより、2つのクイーンが同じファイル(列)にないように処理されます。
- 8つすべての共通表式をクロス結合します。これで、チェス盤に8つのクイーンを置く場合の、可能性があるすべての置き方が生成されます。
- WHERE節により、2つのクイーンが同じランク(行)または同じダイアゴナル上にないことが保証されます。
この照会で、このパズルの92通りのすべての解が見つけられます。
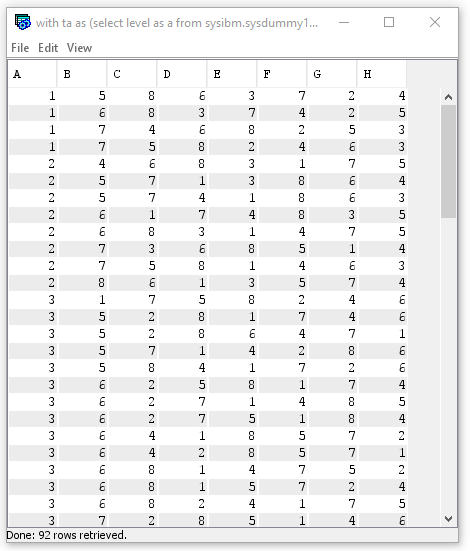
これとは異なる解法を思い付いた方がいらしたら、どうぞお教えください。ぜひとも見てみたいと思います。
エイト クイーン パズルを解くための照会を書くことが実用的であるかどうかは分かりませんが、このことから分かるのは、SQLは、ふだんSQLを使用して行っていることより多くのことを行うことができる、ということなのかもしれません。









